
シャッフルのやり方は十人十色。大会ではどのようなシャッフルが最適かという永遠のテーマを深く掘り下げます。
かなりマニアックな話も多いですし、文章量も多めです。読み飽きたらそこで終了して頂いて構いません。
シャッフルの名称と方法
今回は一般に広く用いられている3つのシャッフル方法を取り上げます。すでに知っている方も多いと思うので、簡単な説明にとどめます。
ディール・シャッフル

山札を任意の数の山に分けた後に、ランダムに重ねるシャッフル方法。上記では10枚に分けていますが、7枚、9枚に分けることもあります。
余談になりますが、積み込みを疑われないために60の約数で分けないようにしましょう。例えば10分けからの6分けを行った場合はシャッフル前の状態に戻ってしまいます。

対戦準備の際によく用いられるシャッフルです。デッキカード枚数確認のためにも利用します。
ヒンズー・シャッフル
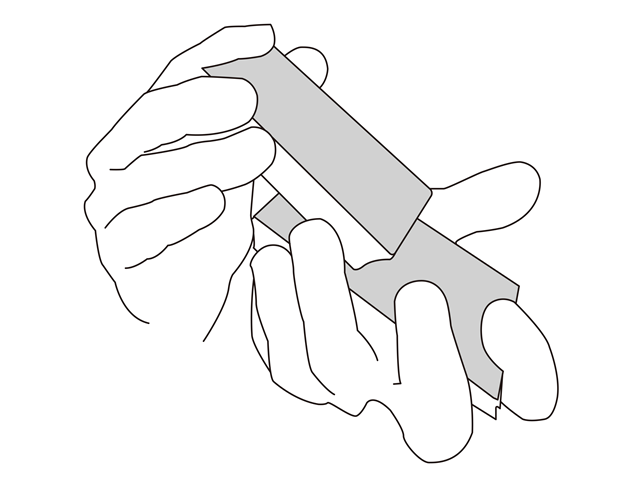
おそらく1番使われているであろうシャッフル方法。1回のシャッフルの時間は短時間で済むため、これを何度も繰り返してシャッフルを行う。
リフル・シャッフル(≒ ファロー・シャッフル)

他のシャッフルに比べるとやや慣れが必要です。上記の画像はファロー・シャッフルですが、類似した方法にリフル・シャッフルがあります。どちらも2つのカードの束を交互に混ざるように行うものであり、混ぜた結果は概ね同じになると言う前提で今後の話は進めていきます。

リフル・シャッフルはカードを反るためダメージが大きく、実際にやることはないでしょう。通常はファロー・シャッフルを行う場面が多いです。
十分にカードを混ぜるために必要な条件は?
・どのカードを引くかプレイヤーが予測できない
・積み込みなどの不正を防止し、公平性を担保する
今回は上記項目が満たせていればゲーム進行する上では問題ないと考えます。以下に引用している文献ではJOKERを除いたトランプ52枚での検証がされています。
ディール・シャッフル単独では不十分
ディールシャッフルを繰り返した場合におけるシャッフル回数mとシャッフルの収束率Cとの関係を下図に示す.数を見るとすべての回数においてC=0.000(0)となっており,シャッフル結果が一意的である(ランダム性がない)という性質が見て取れる。1)
特にmが4の倍数のとき,デッキが元の状態に戻っていることが読み取れる.1)

あくまでも同じ数の束に分けることを繰り返した場合になりますが、時間を要したにも関わらずデッキのランダム性が得られません。

2回目以降のディール・シャッフルの繰り返しは効率が悪い!
ヒンズー・シャッフル単独では時間がかかる
シャッフル回数mと収束率Cとの関係を下図に示す.(中略)m≃50に差し掛かると,これまでのCの伸び率と比較して約倍速でCが増加する(中略).m=86においてC=1.000(2704)を満たした.1)

ヒンズー・シャッフルを86回繰り返せばカードの並びがランダムな状態になるという話です。しかし、これでは1秒で2回シャッフルしても40秒以上要してしまいます。
リフル・シャッフルは効率がいい
「リフルシャッフルを7回行うとデッキがランダムになる」という話は聞いたことがあるでしょうか。トランプ52枚のリフル・シャッフルを繰り返すと、7回目のシャッフルで急にカードがよく混ざるようになる2)ことが研究で示されています。この研究ではカードの全変動距離を用いて、どれくらいシャッフルされているかを見ています。

また、先程のように収束率で評価した場合には以下の結果となっています。
シャッフル回数mと収束率Cとの関係を下図に示す.(中略)m=4からはCの伸び率も緩やかになり、m≧6ではCに大きな変化は現れなくなる.(中略)m=10でC=1.000(2704)となった1)

4回目のリフル・シャッフルで急にカードが混ざるようになり、6回目以降のシャッフルはあまりランダム性に寄与しないことがわかります。

リフル・シャッフル(≒ ファロー・シャッフル)は最低4回行うとカードが混ざりやすいようです。
大会での適切なシャッフルは?
上記の内容をまとめるとリフル・シャッフルに近いファロー・シャッフルが回数が少なくても効率が良くカードが混ざるように思えます。しかし、実際のシャッフルは何種類か方法を混ぜて行います。そして対戦開始前、デッキからのサーチ後、相手デッキカットなど場面に応じて適切なシャッフルは異なるでしょう。
そういったプレイヤーの実情を踏まえての考察を後編の記事で書く予定です。今回は長くなったのでこの辺でいったん終わりにします。
- 井手博康ら, トランプにおける最適なシャッフルの組み合わせ. 情報処理学会論文誌 Vol.59(2018),2054-2062
- Diaconis, P., The cutoff phenomenon in finite Markov chains, Proc. Nat. Acad. Sci. USA, 93 no.4 (1996), 1659–1664.




コメント